All-Zero Block (AZB) Detection for AVC/H.264

This page was inspired by the paper “An Enhanced Detection Algorithm for All-Zero Blocks in H.264 Video Coding”, by Chung-Yen Su.

There are two approaches in development of early-skip methods:

1. necessary skip conditions – if the condition A is met for a block then after transformation and quantization this block is necessarily zero
2. highly likely skip conditions – if the condition B is met for a block then after transformation and quantization this block is highly likely zero

If the first approach is implemented in an encoder there is no impact on visual quality, only the encoding speed boosts (or increases).

However, if you realize the second approach in your early-skip mechanism then there is a penalty in visual quality (due to false positives, if a block is mistakenly considered as skipped), although the encoding speed boosts too.

In this page i consider only methods of the first approach.

The basic idea of AZB (All-Zero Block) is to find methods for early and reliable detection of AZB in order to skip unnecessary transformation and quantization (and inverse transform where needed) and consequently to boost the encoding speed.

It’s worth mentioning that all methods explained below are sufficient methods (i.e. belonging to the first approach). In other words if corresponding conditions are met then the current block is AZB with necessity (no false detentions). Each early AZB detection method of the second approach is always traded between the complexity and the percentage of non-detected AZB.

i outline only two AZB detection methods (both belongs to the first approach): Sousa and Wang methods. These two methods are relevant for 4×4 blocks only.

Sousa’s Method

Let for 4×4 residual block X the following inequality, (S.1) is held then this block is AZB (i.e. all coefficients are zero after quantization):

 

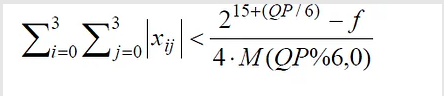
(S.1)

 

 

 

where:

• f is rounding factor. Notice that in the JM reference model software,  f = 2qbits/6 for inter blocks or 2qbits/3 for intra blocks ( qbits = 15 + QP/6 )

• M is the following 6×3 matrix :

 

 

 

 

 

 

 

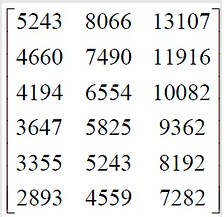
Note: If f is adaptively determined we have to assign the maximal possible magnitude of f in the formula (S.1).

 

Wang’s Method

Let for 4×4 residual block X the following inequality is held then this block is AZB:

 

 

 

 

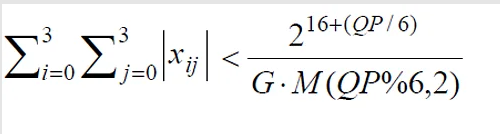
Where G is the largest squared Euclidean norm of the rows of transformation matrix C:

 

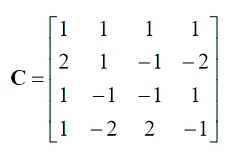
For H.264/AVC 4×4 transformation matrix C,  G = 10.

 

Conclusion:

We described sufficient methods of AZB detection. Each of the above methods misses some percent of real AZBs. Due to lack of false alarms no impact on quality is expected, only the encoding speed can be boosted.

Methods of the second approach give higher AZB detection rates but on contrary they have greater percentage of false alarms (i.e. there is a probability that a block is detected as AZB but it actually is not AZB). Consequently AZB false alarms inevitable impact on video quality.