Use cases from real problems in simplistic form
You are going to verify a SW product by random tests, i.e. you activate a random number generator producing pseudo-random numbers (“pseudo” is not a typo, a deterministic machine can’t produce pure random numbers) say in the range [1..100].
You pick the first 10 random numbers and configure the SW product accordingly (each number corresponding to a predefined preset). However, the random generator produces numbers with replacement, i.e. some numbers may appear several times in a sequence. In such case you may twice or thrice or even more check your SW product in the same mode. It’s redundant.
To avoid duplication of generated pseudo-random numbers you have to keep already obtained random numbers and if the current number has been generated then you activate the random generator again.
1) What’s probability that the list of 10 random numbers from the range [1..100] contain at least one repetition (or duplication)?
This problem is similar to Birthday’s Paradox.
Let’s compute the probability P0 that all random numbers are different (the order in the sequence matters):
P0 = (100)10 /10010 = (1 − 1/100)(1 − 2/100) …. (1 − 9/100) (1)
We simplify the above formula by neglecting cross products (because 10 << 100 ).
P0 ≈ 1 −10·9/200 = 0.55 (1′)
This is very rough approximation, there is better approximation:
What’s is the probability to pick a sample of the length ‘n’ of random numbers (repetitions allowed) from the range [1..N] such that no duplication is present in the sample.
P0 ≈ exp(-n*(n-1)/(2*N)) (2)
For our case n=10 and N=100 we obtain:
P0 ≈ exp(-10*9*/200) = 0.63 (versus 0.55 according the formula (1′))
Thus, the probability for at least one repetition to occur among 10 random numbers from the range [1..100] is ≈ 0.36 .
In such case it’s worth keep already obtained random numbers and to remove duplication (in order to avoid redundant testing of your SW product).
You can generate random numbers by a SW Random Number Generator, however pls. bear in mind these numbers are not really random (they even are called ‘pseudo-random’). Indeed, a deterministic machine can’t in virtue generate real random numbers!!!
If you wish real random figures then you can take two different real dices (not virtual) and roll them, the random number is composed from two digits (first digit is the result of the first dice and the second digit is the result of the second dice respectively). Thus, each roll gives you random numbers in the range [11..66], totally 55 different numbers.
In spirit of the formula (1′) we derive that the probability of a sequence 10 mutually different random numbers obtained by rolling two dices :
P0 ≈ 1 −10·9/110 = 0.18
Hence, the probability of a repetition of random numbers obtaining by rolling of two dices 10 times is ≈ 0.82
Perhaps, rolling of dices is slightly old-fashioned way to fetch real random numbers, i suggest fetching of real random data from www.random.org.
RANDOM.ORG offers true random numbers to anyone on the Internet. The randomness comes from atmospheric noise, which for many purposes is better than the pseudo-random number algorithms typically used in computer programs.
The following python-script fetches random number from 1..100 from random.org
import urllib2
# get random number from 1 to 100
n=20
url = “https://www.random.org/strings/?num=1&len=” + str(n) + \
“&digits=on&upperalpha=on&loweralpha=on&unique=on&format=” \
“plain&rnd=new”
response = urllib2.urlopen(url)
raw = response.read().decode(‘utf8’) # a raw sequence
val = sum(map(ord,raw))%100+1
print(“random value from 1 to 100: %d” %val)
***************************************************************************************************************
2) We generate random numbers in the range [1..100] until a duplication appears. what’s the probability that the process lasts for more than 10 iterations?
The answer: ≈ 1− P0 , where P0 is taken from the formula (1′), ≈ 0.45
***************************************************************************************************************
3) You generate 100 numbers in the range [1..200]. What’s the probability that the number 13 is absent in the 100-element list of random numbers?
We can use Poisson approximation (n=100 is large and p=1/200 is small). Therefore the answer is about e-np= e-0.5 ≈ 0.6
What’s the probability that the number 13 is present exactly one time in the list: 1/2*e-0.5 ≈ 0.3
***************************************************************************************************************
4) A SW program runs 100 times and 8 times crashed. What’s the range of the real failure rate with 95% confidence?
Generally speaking for ‘n’ runs with ‘x’ observed crashes the real failure proportion ‘p’ with 95% confidence lies in the range:
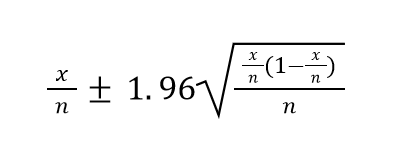
In our case 8 failures from 100 runs the real failure rate with confidence 95% lies in the range [0.026 … 0.13]
8/100 ± 1.96*sqrt(8/100*(1-8/100)/100)
***************************************************************************************************************
5) QA team tested a program several hundred times and got 25% of tests crashed.
A programmer modified the program to decrease the failure rate and delivered the updated program to QA team. QA re-tested the program 24 times only and observed only 3 crashes.
Does the modification decrease the crash rate (or alternatively increase the success rate)?
Let’s formulate the null hypothesis: the success rate is unchanged after the modification and is 75%.
What’s the probability of getting 3 failures or less of 24 tests given the success rate 75%?
The number of successes is binomially distributed Binom(0.75,24). The probability of getting 3 failures or less of 24 tests is expressed in the following formula:

To compute the above formula i recommend to use python module scipy.stats :
from scipy.stats import binom
n = 24
p = 0.75
binom.pmf(21,n,p)+binom.pmf(22,n,p)+binom.pmf(23,n,p)+binom.pmf(24,n,p)
the answer: 0.115
If the significance level of rejection of the null hypothesis (p=0.75) is 0.05, then we can’t reject the null hypothesis that the modification indeed increases the success rate.
6) Your QA engineer said that he ran a program 100 times and 50 times the program was crashed. Assuming that the probability of the program to crash is 50% (hence to succeed is 50% too). This problem is equivalent to finding the probability of tossing a fair coin 100 times and getting 50 heads.
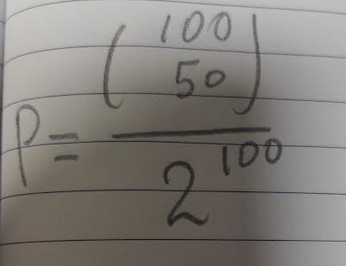
Python code:
import math
p1=float(math.comb(100, 50))/2**100
print(p1)
0.07980868844676221

23+ years’ programming and theoretical experience in the computer science fields such as video compression, media streaming and artificial intelligence (co-author of several papers and patents).
the author is looking for new job, my resume




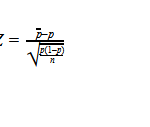


I am in fact pleased to glance at this webpage posts which carries lots of valuable data, thanks for providing these
kinds of data.
Wonderful site. Plenty of helpful information here. I?¦m sending it to a few pals ans also sharing in delicious. And obviously, thanks on your effort!
Greetings from California! I’m bored to tears at work so
I decided to browse your site on my iphone
during lunch break. I love the information you provide here and can’t wait to take a look when I get home.
I’m amazed at how fast your blog loaded on my mobile .. I’m not even using
WIFI, just 3G .. Anyways, great blog!
Thanks on your marvelous posting! I seriously enjoyed reading it, you are
a great author. I will ensure that I bookmark your blog and will eventually come
back later in life. I want to encourage continue
your great posts, have a nice evening!
I believe what you posted was very reasonable. But, what about this?
suppose you were to create a killer headline?
I ain’t saying your information is not good, but suppose you
added a post title that grabbed folk’s attention? I mean Probability Theory and SW Verification – VideoNerd is kinda vanilla.
You ought to peek at Yahoo’s home page and note how they create news
headlines to get viewers interested. You might add a related
video or a picture or two to grab people interested about what you’ve written. Just my
opinion, it would make your posts a little bit more interesting.
it’s not my interest to grab people’s attention. This site is tailored for very narrow ring of specialists and beginners in video compression and media streaming.
Hi, i read your blog occasionally and i own a similar one and i was just
curious if you get a lot of spam remarks? If so how do you prevent
it, any plugin or anything you can suggest?
I get so much lately it’s driving me crazy so any support is
very much appreciated.
this blog is not popular and i don’t obtain too much spam
Hi there! This post couldn’t be written any better! Reading through this post reminds me of my previous room mate! He always kept talking about this. I will forward this article to him. Pretty sure he will have a good read. Thank you for sharing!
I got good info from your blog
I think this is among the most vital info for me. And i am glad reading your article. But wanna remark on some general things, The website style is perfect, the articles is really great : D. Good job, cheers
you are really a good webmaster. The site loading speed is incredible. It seems that you’re doing any unique trick. In addition, The contents are masterpiece. you’ve done a great job on this topic!
Those are yours alright! . We at least need to get these people stealing images to start blogging! They probably just did a image search and grabbed them. They look good though!
of course like your web-site but you have to take a look at the spelling on quite a few of your posts. Several of them are rife with spelling problems and I find it very troublesome to tell the truth however I will surely come again again.
Hello there, I found your website via Google while searching for a related topic, your web site came up, it looks great. I’ve bookmarked it in my google bookmarks.
Great post. I am facing a couple of these problems.
I’ve recently started a web site, the info you offer on this website has helped me tremendously. Thanks for all of your time & work.
Very interesting information!Perfect just what I was looking for!
You have observed very interesting details ! ps decent site.
Great work! This is the type of info that should be shared around the web. Shame on Google for not positioning this post higher! Come on over and visit my website . Thanks =)
Hello videonerd.website administrator, Thanks for the well-organized post!