Software Testing and Statistics (simplified cases from real practice)

1) We often test programs which fails or get stuck  occasionally (e.g. due to a race condition).

Let’s suppose that after a specific fix the failure rate of the program has been reduced – how can we be sure with a high confidence this fix indeed reduces the failure rate and not the result of a random fluctuation?

This question is equivalent to very famous statistics problem – tossing of coin. If we toss a coin 100 times and get the head 63 times.  Can we accept with a high confidence that the probability of getting the head is above 0.5?

Let’s suppose you test a SW program and observe that it sometime is stuck, say 10 of 100 runs the program is stuck. A SW engineer which is responsible for the program adds some fix and now the program is stuck in 5 runs of 100 (i.e. the observed failure rate is reduced twice from 0.1 to 0.05). Can we conclude that this fix indeed improves a reliability of the program and we are in the right way to make the program ‘stuck-free’ (completely reliable)?

In language of statistics we can re-phrase the above question as follows:

Can we with confidence level say 98% accept that the failure rate after the fix is below p=0.1? 

We have two hypotheses:

Null hypothesis H₀:  p=0.1

Alternative hypothesis H_A: p<0.1

 The observed failure rate after the fix is p=0.05, let’s compute the value

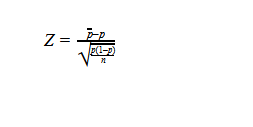
Where n is the number of runs, in our case n=100 and the null-hypothesis  p=0.1.

We reject the null hypothesis (or in other words we accept the alternative hypothesis that the fix helps) if Z <-2.05 (since the left-tailed Z for α=0.02 is -2.05 or the confidence level is 98%).

In our case with  p=0.05 and n=100 we have Z=-1.6. Hence, we can’t infer with the confidence above 98% that the fix indeed helps.

 

Let’s suppose that the SW engineer makes another fix and we obtained better results: 3 failures of 100 (i.e. is p=0.03). In such case Z = -2.3 < -2.05 and hence we can infer with the confidence above 98% that the last fix indeed reduces the failure rate.

 

2) A program is tested 7 times and after a number of hours it’s crashed. An engineer added some changes in the program and the number of hours before crashes increased (from 7 tests 6 times crashes were observed lately than in the original version). Can we accept that the changes in the program indeed helped?

Tests	1	2	3	4	5	6	7
Before change working in hours until crashed	15	23	32	29	28	24	13
After change	22	26	38	33	30	28	10

 

The null hypothesis: the modification in the code does not impact. Under the null hypothesis what’s the probability that 6 of 7 tests show longer running?

The probability (P-value) of getting such result or better:  7/128 + 1/128 = 6.25% . We can’t reject the null hypothesis with 5% confidence.