Stability of System Linear Equations and Condition Number

Let’s consider the system of linear equations in the matrix form:   A x = b

If we make tiny changes in the vector ‘b’ and the solution ‘x’ will change a little then the matrix ‘A’ is called stable. Otherwise, if any tiny change of the vector ‘b’ provides strongly different solution ‘x’, then the matrix ‘A’ is called unstable or ill-conditioned. 

 

Example of ill-conditioned matrix:

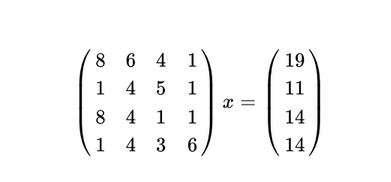
# python script

import numpy as np

A = np.array([[8,6,4,1],[1,4,5,1],[8,4,1,1],[1,4,3,6]])
b = np.array([19,11,14,14])
x=np.linalg.solve(A,b)
print(‘solution:’)
print(x)

solution:
[1. 1. 1. 1.]

# perturb the vector ‘b’ by adding 0.01

b = np.array([19.01,11.01,14.01,14.01])

x=np.linalg.solve(A,b)
print(‘perturbed solution:’)
print(x)

perturbed solution:
[0.8 1.525 0.65 0.86 ]

 

Example of stable matrix:

# generate stable matrix as random integers in the range 1..100

A = np.random.randint(100,size=(5,5))
print(A)
b = np.random.randint(100,size=(5,1))
print(b)

 

 

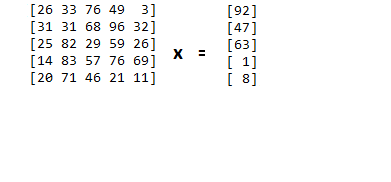
# find solution ‘x’

x=np.linalg.solve(A,b)
print(‘solution:’)
print(x)

solution:
[[-16.61183254]
 [  3.32568748]
 [  1.32647771]
 [  6.96962099]
 [ -9.38792507]]



# perturb the vector 'b' by adding 0.01
b=b+0.01
x=np.linalg.solve(A,b)
print('perturbed solution:')
print(x)

perturbed solution:
[[-16.61161905]
 [  3.32573675]
 [  1.32653263]
 [  6.96959163]
 [ -9.38789576]]

 

 

How determine stability of the matrix?

Compute the condition number:

where λ₁ is the maximum singular value of and λ_n is the smallest.

The higher the condition number, the more unstable the system (more sensitive to perturbations).

The following script calculates the condition number

 

• for ill-conditioned matrix A from the first example, the condition number equal:

_, s, _ = np.linalg.svd(A)
print(‘Condition number of A: ‘, max(s)/min(s))

Condition number of A: 3198.6725811994825

• for stable matrix A from the second example, the condition number equal:

Condition number of A: 55.00882596574336