In Theory of Graphs there is the following theorem:
A graph with more than two vertexes has at least two vertexes with the same degree. Proof
Let’s consider a party where each guest is a vertex. Two vertexes (or guests) are connected if they are acquaintances. The theorem asserts that in each party above two guests there are at least two guests with the same number of acquaintances (0 acquaintances is also considered).

23+ years’ programming and theoretical experience in the computer science fields such as video compression, media streaming and artificial intelligence (co-author of several papers and patents).
the author is looking for new job, my resume

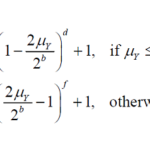



Amazing! This blog looks exactly like my old one! It’s on a totally different subject but it has pretty much the same page layout and design. Excellent choice of colors!
I simply could not leave your web site before suggesting that I actually loved the usual info an individual provide in your visitors? Is gonna be back incessantly to check out new posts.
Cool blog! Is your theme custom made or did you download it from somewhere? A design like yours with a few simple adjustements would really make my blog jump out. Please let me know where you got your design. Thank you
it’s a famous problem
whoah this blog is wonderful i like reading your articles. Stay up the great work! You understand, a lot of persons are looking around for this information, you can help them greatly.
very nice submit, i actually love this website, keep on it
Some really wonderful work on behalf of the owner of this site, dead great articles.
What i don’t realize is if truth be told how you are not actually much more well-appreciated than you may be now. You’re very intelligent. You know therefore considerably on the subject of this matter, produced me in my opinion consider it from a lot of numerous angles. Its like men and women aren’t fascinated except it is something to do with Lady gaga! Your individual stuffs outstanding. At all times take care of it up!
Well I truly liked reading it. This post provided by you is very useful for accurate planning.
I¦ve been exploring for a bit for any high quality articles or weblog posts on this sort of space . Exploring in Yahoo I eventually stumbled upon this web site. Studying this info So i am happy to show that I’ve a very just right uncanny feeling I came upon exactly what I needed. I so much definitely will make certain to don¦t put out of your mind this site and provides it a glance on a constant basis.
I believe other website owners should take this website as an example , very clean and superb user pleasant style and design.